Percentage & Percentage change

Percent (read as per cent) means ‘every hundred’, or, essentially, ‘out of 100’. If we are given a fraction, we can simply convert it to a percentage by multiplying 100. Say, we have ½, which, when multiplied with 100 becomes ½ x 100 = 50%.

What do we mean by a percentage change?

Say, a person has 20 chocolates. If his number of chocolates is increased by 10%, what does it mean? First of all, let us see what is doesn’t mean: after the increase, the number of chocolates with him is NOT 20 + 10 = 30, nor is it 20 + ¹⁰/₁₀₀ = 20.1

When we talk of a percent increase, we must understand on what BASE VALUE is the percentage change working on. In this case, obviously, the 10% increase is 10% of the number of chocolates he has, i.e. 20. Thus, the number of chocolates with him would become:

20 + 10% of 20 = 20 + 20 x ¹⁰/₁₀₀ = 22

Observe that: 20 + 20 x ¹⁰/₁₀₀ = 20 x (1 + ¹⁰/₁₀₀) = 20 x (1 + ¹/₁₀) = 20 x (¹¹/₁₀) = 20 x 1.1

Thus, a 10% increase is essentially an increase of (¹/₁₀)^th which basically means a multiplication with ¹¹/₁₀ or 1.1; we can use either value depending on the convenience of using a decimal number or using a fraction.

Below is a list of certain percent values and the corresponding number with which to multiple for a corresponding percentage increase or decrease:

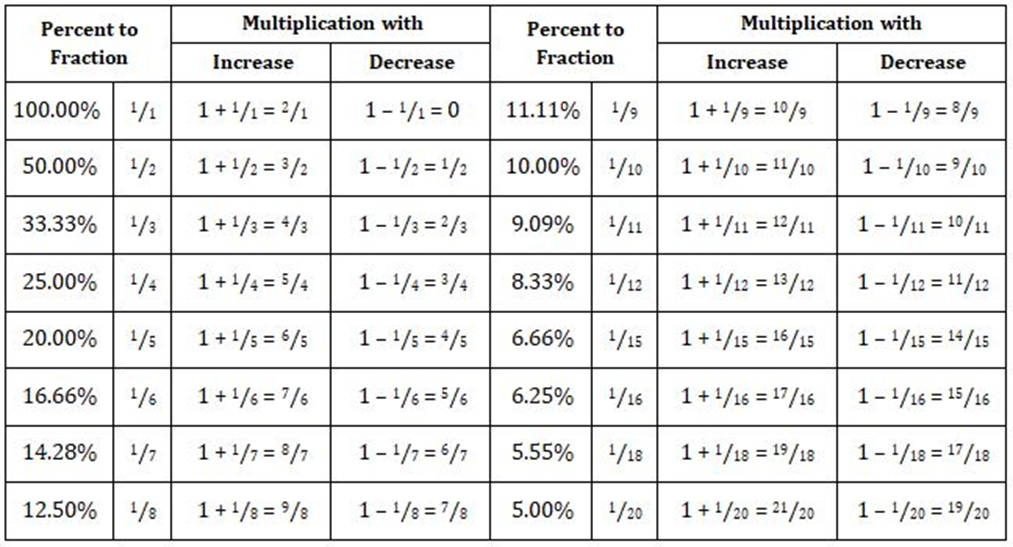
We have seen above, that, for a given percentage change, we can calculate the final value. However, if the initial and final values are known, how do we calculate percentage change?

 Percentage change is simply the change in value taken as a percentage of the initial value. Thus:

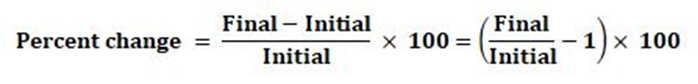
Note that the ratio of the ‘Final’ and ‘Initial’ values is the same as the number with which we multiply in case of a given percent change (shown in the table above).

For any queries regarding the courses, feel free to talk to our mentors and our counselors. You may book a free counseling session and reach us at +919433063089