GMAT Quant – Ten points to keep in mind

The Graduate Management Admission Test (GMAT) is a computer adaptive test taken for entry into top management programs worldwide. It is intended to assess the student’s ability in the Verbal Ability and Quantitative Aptitude along with writing and data analysis skills.

Being adaptive in nature, the test puts forward questions depending on the solving accuracy of the candidate in previous questions. The questions are also tricky, enticing a candidate to make inadvertent mistakes. We have listed down ten most important strategies to follow while tackling the quant section of the GMAT – we have also solved some questions to drive the point home. Before going through the solutions, try to solve the questions and then verify the approach with the explanations provided.

Do not make assumptions while solving a problem

As already mentioned, most GMAT questions have some trick element which is often overlooked by the students. Also, the wording is such that the students make assumptions which they feel are obviously true. Thus, students often end up misinterpreting the question and get an incorrect answer.

Example 1: If x > 7 and y > 9, what is the least integer value of (x + 2y)?
A. 25
B. 26
C. 27
D. 28
E. 29

Explanation:
x > 7 … (i)
y > 9 => 2y > 18 … (ii)
Adding (i) and (ii):
x + 2y > 7 + 18
=> x + 2y > 25
Thus, the least integer value is 26 (Option B)

A common mistake here is to assume that x and y are integers (though that hasn’t been mentioned) and using the values: x = 8 and y = 10, thereby getting x + 2y = 28

Use estimation strategies – comparison, units digit, options

In the GMAT, we usually never need to execute complex calculations. Even if a calculation looks complex, we can approximate the values or come up with other ways to determine the correct answer without actually having to execute a long calculation. Let us look at a few examples.

Example 2:
What is the value of the calculation below: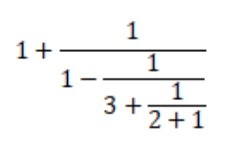

A. 7/11
B. 9/10
C. 7/6
D. 13/7
E. 17/7

Explanation:
The first instinct is to start calculating the value.
However, if you observe the calculation given, the answer must be greater than 1. The rules out options A and B.
Next, if you observe the part: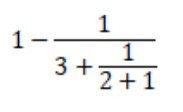

We see that this is definitely smaller than 1.
Thus, the reciprocal of this is greater than 1.
Hence, the overall value is 1 added to something greater than 1; hence is greater than 2.
There is only one option greater than 2, Option E.

Example 3:
Which of the following options satisfies the value below:
S = 1/2 – 1/4 + 1/8 – 1/16 + 1/32 … till 20 terms?
A. S > 2
B. 1 < S < 2
C. 1/2 < S < 1
D. 1/4 < S < 1/2
E. S < 1/4

Explanation:
Here, even if you try adding the first 5 or 6 terms, you will understand that it isn’t something you want to do!
So let us approach in a different manner.
If we ignore the first term and group every pair of terms thereafter, we observe:
-1/4 + 1/8 < 0
-1/16 + 1/32 < 0, and so on
Thus, the sum is definitely
smaller than 1/2 … (i)

If we now combine every pair of terms starting from the first term, we observe:
1/2 – 1/4 = 1/4
1/8 – 1/16 > 0
1/32 – 1/64 > 0, and so on
Thus, the sum is definitely greater than 1/4 … (ii)

Hence, the answer is Option D.

Example 4:
Which of these is equal to 10!×5!?
A. 43578600
B. 256589200
C. 416784000
D. 435456000
E. 459860000

Explanation:
This is clearly an example where the calculation is too lengthy to execute.
Let us try another way.
We know that 10! has 5² as a factor and 5! has another 5 as a factor. Thus, the product will have 5³ as a factor.
Since the number of 2s will be way higher, each 2 will combine with a 5 resulting in 10³.
Thus, the product will definitely have 3 zeroes at the end.
Thus, only options C and D are possible.
Let us now calculate the units digit of the product (we will ignore the three 2s and the the three 5s above):

Thus, 10! × 5!
= 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 × 10 × 1 × 2 × 3 × 4 × 5
We have to remove three 2s and three 5s, so we remove 4, 5, 5 and 10, leaving us with:
1 × 2 × 3 × 6 × 7 × 8 × 9 × 1 × 2 × 3 × 4
The units digit of this product is 6
Thus, the required answer must have 6000 at the end – Option D

Use numbers to solve questions

Often, plugging in numbers to check whether a relationship holds or not is a quick and effective way to solve a question.
Let us look at this example:

Example 5:
If n > n², which of the following may be true?
I. n² > n³
II. n³ > n²
III. n³ > n
A. Only I
B. Only III
C. Both I and III
D. Both II and III
E. I, II and III

Explanation:
For this question, we need to understand that there are 4 major parts of the number line

Greater than 1
Between 0 and 1
Between 0 and -1
Smaller than -1

Let us use a number from each region and verify the three statements.

Greater than 1: n = 2 doesn’t satisfy n > n², hence is discarded
Between 0 and 1: n = 1/2 satisfies n > n²
I: n = 1/2 satisfies n² > n³. Thus, I is possible
II: n = 1/2 doesn’t satisfy n³ > n², hence is discarded
III: n = 1/2 doesn’t satisfy n³ > n², hence is discarded
Between 0 and -1: n = -1/2 doesn’t satisfy n > n², hence is discarded
Less than -1: n = -2 doesn’t satisfy n > n², hence is discarded

Thus, only statement I is possible – Option A

Let us take another example to show how the choice of a starting number simplifies the solution process.

Example 6:
A store sold 2 items whose costs were in the ratio 2:3. The first item was sold at a profit of 33.33% while the selling price of the second item was 25% higher than the selling price of the first item. What was the overall profit percentage?
A. 16.67%
B. 20%
C. 25%
D. 27.5%
E. 33.33%

Explanation:
We know that 33.33% corresponds to the fraction 1/3 and 25% corresponds to the fraction 1/4.
Since the profit is 33.33%, we need to take 1/3 times the cost to calculate the profit. Thus, to make the calculation simple, we multiply the cost price ratio 2:3 with 3 and make it 6:9, i.e. assuming cost of the first item is $6 and that of the second is $9.
Thus, profit made on the first item is 1/3 × $6 = $2, hence the selling price of the first item is $8.
Thus, selling price of the second item is $8 + 1/4 × $8 = $10

Thus, total cost price = $6 + $9 = $15, whereas the total selling price = $8 + $10 = $18. Thus, there is a profit of $3.
Thus, profit percentage = 3/15 × 100 = 20% – Option B

Learn to factorize – divisibility rules, patterns, algebraic identities

Factorization is something that is useful is diverse areas. We need it in determining the factors of a number, computing the GCD and LCM, and even while trying to simplify a calculation. Let us take some examples to see different ways in which factorization can be done.

Example 7:
Which of the following is NOT a factor of 5⁸ – 2⁸?
A. 3
B. 7
C. 21
D. 29
E. 31

Explanation:
We will use a few algebraic identities here:
a² – b² = (a – b)(a + b)
Thus, we have:
5⁸ – 2⁸
= (5⁴ – 2⁴) × (5⁴ + 2⁴)
= (5² – 2²) × (5² + 2²) × (5⁴ + 2⁴)
= (5 – 2) × (5 + 2) × (5² + 2²) × (5⁴ + 2⁴)

Thus, the factors are:
5 – 2 = 3
5 + 2 = 7
5² + 2² = 25 + 4 = 29
5⁴ + 2⁴ = 625 + 16 = 641
Hence, Option E is correct

Simplify and avoid long calculations

The trick is calculations is to not calculate the value at each step, rather try to compute the answer at the very last step. That way, a lot of factors can cancel out simplifying the calculation.
Under any circumstances, avoid the use of a calculator since you won’t get one in the actual test. Let us take an example.

Example 8:
At the end of his two-year investment, the net value Chandler received was $4410. If the investment paid an annual interest of 5 percent, what was the amount of money that Chandler originally invested?
A. $3600
B. $3840
C. $4000
D. $4200
E. $5000

Explanation:
Let us assume the investment to be $P
Since 5% is equivalent to the fraction 1/20, we have:
The net value of the investment after 2 years
= $P × (1 + 1/20) × (1 + 1/20)
= $P × (21/20)²
Note that we are not computing the value (21/20)² and letting it be.

Thus, we have:
P × (21/20)² = $4410
P = $4410 × (20/21) × (20/21)
We will now do the calculation and observe that 21 × 21 = 441 (or we can factorise 4410 and cancel common terms)

Thus, we have:
P = $4410 × 400/441 = $4000 – Option C

Use logic over formulae

In the GMAT, understanding the logic is paramount; the knowledge of formulae is secondary. Students would be able to solve problems faster if they focus on the concept and logic rather than formulae. This is particularly true for Arithmetic problems involving percentages, rate and work, speed and distance, averages and ratios. Also, option choices can be very effectively used to arrive at the correct option by the process of elimination.

The Data Sufficiency Trap

Data Sufficiency is tricky by nature. It is unfamiliar to many students and demands lateral thinking. Fortunately, the mistakes one makes in these questions can be avoided with practice. The most common mistake students make is they make unwarranted assumptions and also confuse the information mentioned in the statements.
Also, in Data Sufficiency, you do not necessarily have to solve the question; you just need to check whether the statements are sufficient to solve the question.
Let us take an example.

Example 9:
In 2020, the profits of a company were 20% greater than that in 2019. In 2019 the profits of the company were 30% greater than that in 2018. What were the company’s profits in 2019?
(1) In 2020, the company’s profits were $36000 greater than that in 2017.
(2) The profit of the company in 2019 was 50% higher than that in 2017.

Explanation:
We can see that there are 4 different years being talked about.
Since we need the (dollar) value of the profit, clearly statement 2 alone is not sufficient since it does NOT offer any dollar value (the stem of the question also does not offer any dollar value).
Let us now focus on the question stem and on statement 1:
Assuming the profit in 2018 to be $x, we have:
Profit in 2019 = $1.3x
Profit in 2020 = 1.2 × $1.3x = $1.56x (some value in terms of x)
Profit in 2017 = $1.56x – 36000
Thus, we know the profits in each of the years in terms of a variable, but we have no way to compute the value of the variable – Insufficient
Note: The calculations above is NOT important, but the understanding that you can obtain all the profits in terms of a single variable is important.

Combining the statements:
We now have the missing relation using which we can calculate the value of x:
The profit of the company in 2019 was 50% higher than that in 2017
1.3x = 1.5 × (1.56x – 36000)
Since we CAN solve for x from this equation and that value will also be unique, we CAN definitely compute the profit in 2019 – Sufficient
Note that trying to solve for x is unnecessary and a waste of time. Gradually, with practice, you should be able to visualise the data well enough to be able to come to such conclusions faster.

Thus, the answer is Option C (combining both statements)
Another tip: You should make sure that you know exactly which option means what in data sufficiency questions so that you do not have to refer to the instructions each time.

Do not waste too much time on a question

In a timed test like the GMAT, it is important that one doesn’t lose track of time. If confronted with a very difficult question or a question where you feel stumped, the best way to proceed is to use logic, and along with the option choices eliminate a few of the options and mark what appears to be the best option.
Whenever you find that after spending more than two or three minutes, there is no progress, it is best to proceed as discussed above.

Have confidence – don’t try to cross check every answer

To ensure high accuracy, students often waste too much time on a single question. They end up reading the same question multiple times and solving the same question in different ways trying to confirm the answer. Also, if a question seems easy, they end up scrutinizing it thinking there is some trap. This behavior disturbs the time available for the other problems in the section.

Learn the concepts

Though mentioned at the end, this is the most important point. No strategy will work if your concepts are not in place.
For example, if you have no idea what a slope signifies, you will either get the following question wrong or end up taking a long time to solve.

Example 10: C = 9F/5 + 32 is the equation used to convert temperature measured in Fahrenheit (F) to Celsius (C). If the temperature of an object changes by 25^o F, what would be the corresponding change in degree Celsius?
A. 13^o C
B. 25^o C
C. 45^o C
D. 77^o C
E. 80^o C

Explanation:
A common mistake is to substitute F = 25 in the equation and determine C = 77

We need to understand that the equation:
C = (9/5)F + 32 is essentially:
y = mx + b, where y is C, x is F and m = 9/5
Thus, 9/5 equals the ratio of the change in C to the change in F
Since the change in F is 25^o, we have:

(Change in C)/25 = 9/5
=> Change in C = 9/5 × 25 = 45 (Option C)

Hopefully this article and the examples have provided some idea about how to tackle the Quant section of the GMAT. If you are thinking to take the GMAT in the future, we suggest you focus on the basic concepts and build a preparation strategy that ensures high accuracy. At OneClick Prep, we make sure that the basic concepts are adequately stressed upon. Also, with over a couple of thousand practice problems, we make sure that your GMAT preparation is right up to the mark.

Have questions? Call us for a free consultation regarding your career moves – be it MBA in India or study abroad programs through GMAT or GRE. Call us: +91 9433063089